Heptagonaaliset prisman ominaisuudet ja kuinka lasketaan tilavuus
heptagonaalinen prisma on geometrinen kuva, joka, kuten nimikin viittaa, käsittää kaksi geometrista määritelmää, jotka ovat: prisma ja heptahoni.
"Prisma" on geometrinen kuva, joka on rajoitettu kahteen perustaan, jotka ovat yhtäläisiä ja rinnakkaisia monikulmioita, ja niiden sivupinnat ovat rinnan suuntaisia.
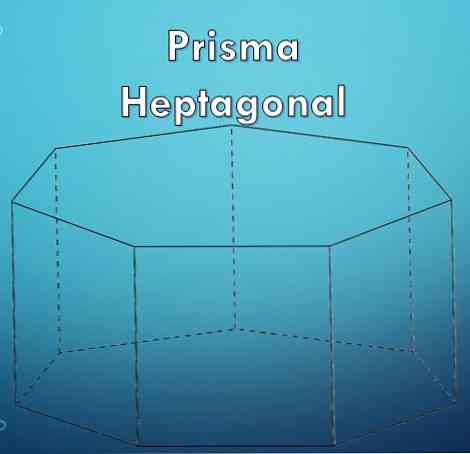
"Heptagon" on monikulmio, jonka muodostavat seitsemän (7) puolta. Koska heptagon on monikulmio, voi olla, että se on säännöllinen tai epäsäännöllinen.
Monikulmion sanotaan olevan säännöllinen, jos kaikilla sen sivuilla on sama pituus ja niiden sisäiset kulmat ovat samoja, niitä kutsutaan myös tasasivuisille polygoneille; muuten sanotaan, että monikulmio on epäsäännöllinen.

Heptagonaalisen prisman ominaisuudet
Seuraavassa on tiettyjä piirteitä, joilla on heptagonaalinen prisma, kuten: sen rakenne, sen pohjaan liittyvät ominaisuudet, kaikkien kasvojen alue ja tilavuus.
1- Rakentaminen
Heptagonaalisen prisman rakentamiseksi tarvitaan kahta heptagonia, jotka ovat sen pohjat ja seitsemän rinnakkaismittaria, joista toinen on heptaanin kummallakin puolella.
Aloita piirtämällä heptagonia, sitten vetämällä seitsemän pystysuoraa linjaa, jotka ovat yhtä pituisia ja tulevat jokaisesta sen huippuista.
Lopuksi piirretään toinen heptagon, niin että sen huiput yhtyvät edellisessä vaiheessa piirrettyjen viivojen loppuun.
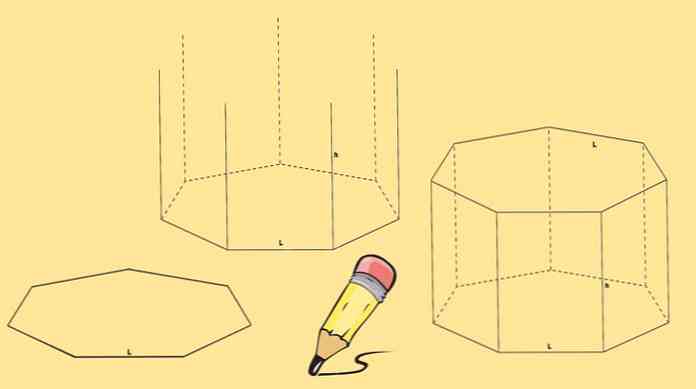
Edellä kuvattua heptagonaalista prismaa kutsutaan suoraksi heptaaliseksi prismaksi. Mutta sinulla voi olla myös vinonhehkulmainen prisma, kuten seuraavassa kuvassa.

2- Sen perusasioiden ominaisuudet
Koska niiden emäkset ovat heptagoneja, ne täyttävät, että diagonaaliluku on D = nx (n-3) / 2, jossa "n" on monikulmion sivujen lukumäärä; tässä tapauksessa D = 7 × 4/2 = 14.
Voimme myös nähdä, että minkä tahansa heptagonin (säännöllinen tai epäsäännöllinen) sisäisten kulmien summa on yhtä suuri kuin 900º. Tämä voidaan tarkistaa seuraavalla kuvalla.
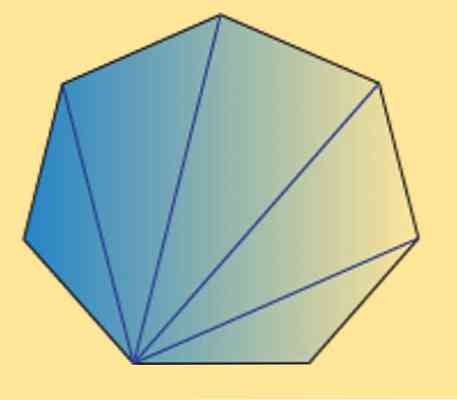
Kuten näette, on 5 sisäistä kolmiota, ja käyttämällä kolmion sisäisten kulmien summaa 180 °, voidaan saavuttaa haluttu tulos.
3 - Heptagonaalisen prisman rakentamiseen tarvittava alue
Koska sen emäkset ovat kaksi heptagonia ja sen sivut ovat seitsemän rinnakkaismittaria, heptagonaalisen prisman rakentamiseen tarvittava alue on yhtä suuri kuin 2xH + 7xP, jossa "H" on kunkin heptagonin alue ja "P" jokaisen rinnakkaisohjelman pinta-ala.
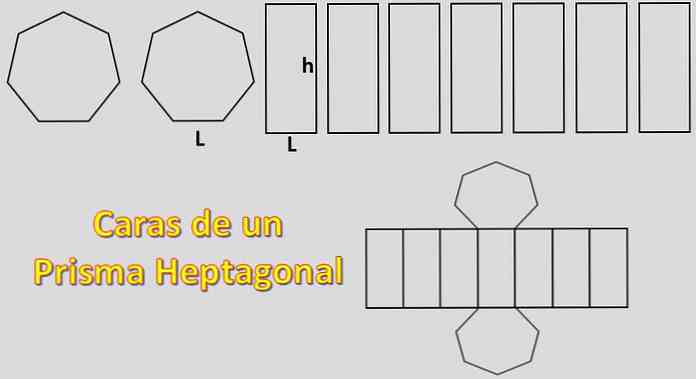
Tällöin lasketaan tavallisen heptagonin pinta-ala. Tätä varten on tärkeää tietää apoteman määritelmä.
Apothem on kohtisuorassa linjassa, joka kulkee säännöllisen monikulmion keskeltä minkä tahansa sen sivun keskipisteeseen.
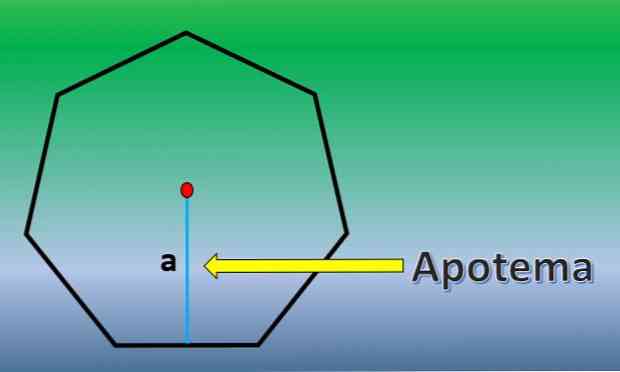
Kun apothem on tunnettu, heptagonin pinta-ala on H = 7xLxa / 2, jossa "L" on kunkin sivun pituus ja "a" apothemin pituus..
Rinnakkaisohjelman pinta-ala on helppo laskea, se on määritelty P = Lxh, jossa "L" on sama pituus heptagonin sivussa ja "h" on prisman korkeus..
Yhteenvetona voidaan todeta, että heptagonaalisen prisman rakentamiseen tarvittavan materiaalin määrä (säännöllisesti) on 7xLxa + 7xLxh eli 7xL (a + h).
4- Volume
Kun pohjapinta-ala ja prisman korkeus ovat tiedossa, tilavuus on määritelty (perusala) x (korkeus).
Heptagonaalisen prisman (jossa on tavallinen pohja) tapauksessa sen tilavuus on V = 7xLxaxh / 2; voidaan kirjoittaa myös nimellä V = Pxaxh / 2, jossa "P" on tavallisen heptaanin kehä.
viittaukset
- Billstein, R., Libeskind, S., & Lott, J. W. (2013). Matematiikka: perusopetuksen opettajien ongelmanratkaisu. López Mateos Editorit.
- Fregoso, R. S., & Carrera, S. A. (2005). Matematiikka 3. Toimituksellinen Progreso.
- Gallardo, G., ja Pilar, P. M. (2005). Matematiikka 6. Toimituksellinen Progreso.
- Gutiérrez, C. T. ja Cisneros, M. P. (2005). 3. matematiikan kurssi. Toimituksellinen Progreso.
- Kinsey, L., & Moore, T. E. (2006). Symmetria, muoto ja tila: Johdatus matematiikkaan geometrian kautta (havainnollistettu, uusintapainos.). Springer Science & Business Media.
- Mitchell, C. (1999). Häikäisevät Math Line -mallit (Illustrated ed.). Scholastic Inc.
- R., M. P. (2005). Piirrän 6º. Toimituksellinen Progreso.


