Kulmansiirtymämuodot ja ratkaisut

kulmakulma se syntyy, kun objekti liikkuu polun tai polun, joka on ympyrän muotoinen, jälkeen. Se eroaa siirtymästä; kun kulman siirtymä mittaa kulman kulman, siirtymä mittaa etäisyyden.

Kehän ympärysmittaan liikkuvan kohteen kulman siirtymisen laskemiseksi voidaan käyttää kahta tapaa: jos alku- ja loppukulma tunnetaan, kulmakulma on lopullisen kulman ja alkukulman välinen vähennys.

Jos siirtymän pituus (kehän kaaren pituus kulkee) ja kehän säde ovat tiedossa, kulmansiirtymä on θ = l / r.

indeksi

• 1 Kaavat
• 2 Harjoitukset
  • 2.1 Ensimmäinen harjoitus
  • 2.2 Toinen harjoitus
  • 2.3 Kolmas harjoitus
• 3 Viitteet

kaavat

Saadaksesi yllä kuvatut kaavat voit nähdä seuraavat kuvat:

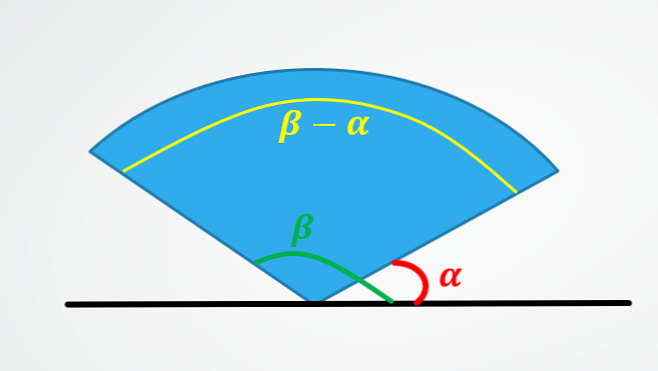
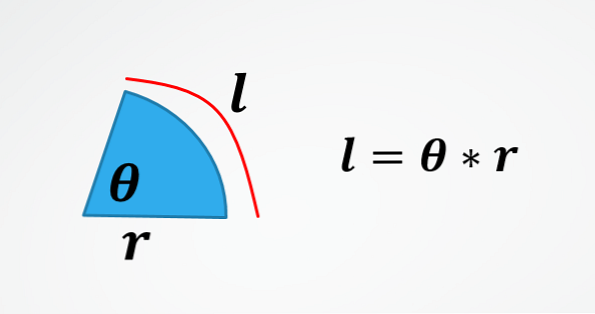
Ensimmäinen osoittaa, miksi kulmakulma on yhtä suuri kuin lopullisen kulman vähennys miinus alkukulma.

Toisessa kuvassa on kaavan kaaren kaavan kaava. Näin ollen selvittämällä θ saat alussa kuvatun kaavan.

koulutus

Alla on muutamia harjoituksia, joissa tulisi käyttää kulma-asennon määritelmää ja jossa käytetään edellä kuvattuja kaavoja.

Ensimmäinen harjoitus

Juan on kulkenut 35 metrin etäisyydellä pyöreältä juoksuradalta, jonka säde on 7 metriä. Laske Juanin tekemä kulmakulma.

ratkaisu

Koska tunnetun kaaren etäisyys ja kehän säde ovat tiedossa, voidaan toista kaavaa soveltaa Juanin tekemän kulman siirtymän tuntemiseen. Käyttämällä yllä kuvattua kaavaa sinulla on θ = 35/7 = 5 radiaania.

Toinen harjoitus

Jos sinulla on, että Mario on matkustanut autossaan puolet pyöreästä kilparadasta, mikä on Mario-kulman kulma, jota Mario on tehnyt??

ratkaisu

Tässä harjoituksessa käytetään ensimmäistä kaavaa. Koska tiedetään, että Mario on kulkenut puolet radasta, voidaan olettaa, että hän aloitti kilpailun 0 ° kulmassa ja kun hän pääsi ympyrän keskelle, hän on kulkenut 180 °. Siksi vastaus on 180 ° -0 ° = 180 ° = π radiaania.

Kolmas harjoitus

Marialla on pyöreä allas. Koirasi kulkee altaan ympärillä, joka on 18 metrin päässä. Jos uima-altaan säde on 3 metriä, mikä on Maria-maskotin tekemä kulmakulma??

ratkaisu

Koska allas on pyöreä ja tiedät sen säteen, voit jatkaa toisen kaavan käyttöä.

Tiedetään, että säde on 3 metriä, ja lemmikkieläimen kuljettama matka on 18 metriä. Sen vuoksi suoritettu kulma- siirtymä on yhtä suuri kuin θ = 18/3 = 6 radiaania.

viittaukset

1. Basto, J. R. (2014). Matematiikka 3: Analyyttinen geometria. Patrian toimittajaryhmä.
2. Billstein, R., Libeskind, S., & Lott, J. W. (2013). Matematiikka: perusopetuksen opettajien ongelmanratkaisu. López Mateos Editorit.
3. Bult, B., & Hobbs, D. (2001). Matematiikan sanakirja (kuvitettu ed.). (F. P. Cadena, Trad.) Julkaisut AKAL.
4. Callejo, I., Aguilera, M., Martinez, L., & Aldea, C. (1986). Math. Geometria. E.G.B: n ylemmän syklin uudistaminen. Opetusministeriö.
5. Schneider, W. & Sappert, D. (1990). Käytännön tekninen piirustusopas: johdanto teollisen teknisen piirustuksen perusteisiin. Reverte.
6. Thomas, G. B., ja Weir, M. D. (2006). Laskeminen: useita muuttujia. Pearson Education.