Kuinka monta Symmetria-akselia Circle on?

ympyrän symmetria-akselit Ne ovat ääretön. Nämä akselit ovat ne, jotka jakavat geometrisen muodon kahteen täsmälleen yhtä suureen puolikkaaseen.

Ja ympyrä koostuu kaikista pisteistä, joiden etäisyys kiinteään pisteeseen on pienempi tai yhtä suuri kuin tietty arvo "r".

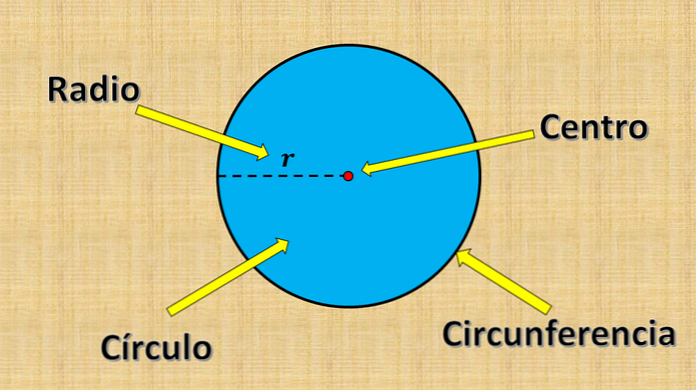
Edellä mainittua kiinteää pistettä kutsutaan keskustaksi, ja arvoa "r" kutsutaan sädeeksi. Säde on suurin etäisyys, joka voi olla ympyrän pisteen ja keskuksen välillä.

Toisaalta halkaisijaksi kutsutaan mikä tahansa viivasegmentti, jonka päät ovat ympyrän reunalla (ympärysmitta) ja jotka kulkevat keskuksen läpi. Sen mittaus on aina yhtä suuri kuin kaksinkertainen säde.

Ympyrä ja ympärysmitta

Älä sekoita ympyrää ympyrän kanssa. Kehä viittaa vain pisteisiin, jotka ovat etäisyydellä "r" keskustasta; eli vain ympyrän reuna.

Kun etsit symmetria-akseleita, on kuitenkin välinpitämätöntä, jos työskentelet ympyrän tai ympyrän kanssa.

Mikä on symmetria-akseli?

Symmetria-akseli on linja, joka jakaa kahteen yhtä suureen osaan tietyn geometrisen kuvan. Toisin sanoen symmetria-akseli toimii kuin peili.

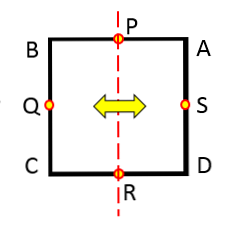
Ympyrän symmetria-akselit

Jos havaitset mitä tahansa ympyrää, sen sädekuvasta riippumatta, näet, ettei jokainen rivi, joka ylittää sen, on symmetria-akseli.

Esimerkiksi yksikään seuraavassa kuvassa piirretyistä viivoista ei ole symmetria-akselia.

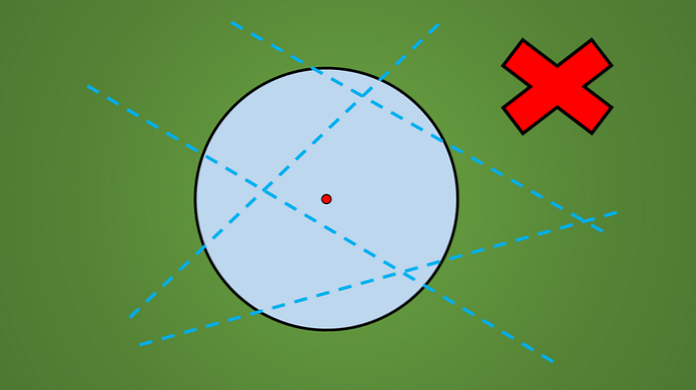
Helppo tapa tarkistaa, onko linja symmetria-akseli vai ei, on heijastaa kohtisuoraan geometrista kuvaa linjan vastakkaiselle puolelle.

Jos heijastus ei sovi alkuperäiseen kuvaan, kyseinen viiva ei ole symmetria-akseli. Seuraava kuva kuvaa tätä tekniikkaa.

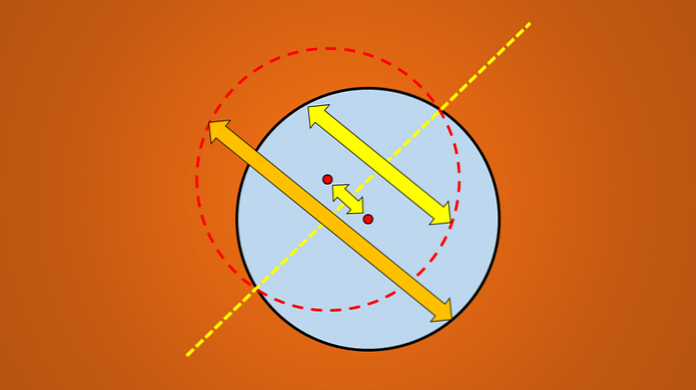
Mutta jos otetaan huomioon seuraava kuva, on hyvin tunnettua, että piirretty viiva on ympyrän symmetria-akseli.

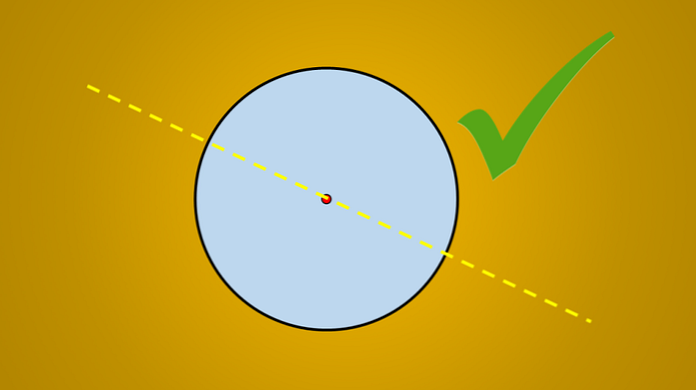
Kysymys kuuluu: ovatko useampia symmetria-akseleita? Vastaus on kyllä. Jos käännät tätä viivaa 45 ° vastapäivään, saatu viiva on myös ympyrän symmetria-akseli.

Sama tapahtuu, jos pyörät 90 °, 30 °, 8 ° ja yleensä minkä tahansa määrän astetta.

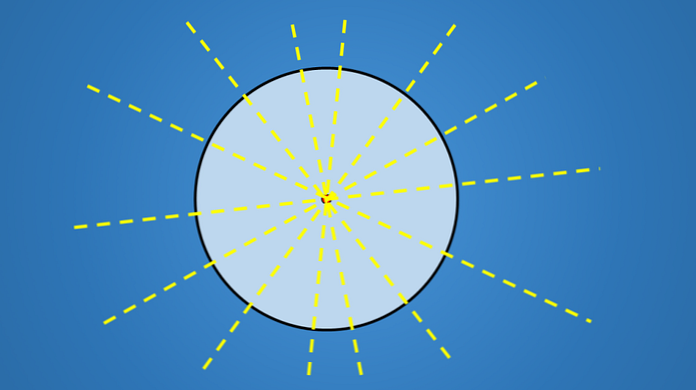
Näillä linjoilla ei ole tärkeää, että heillä on kaltevuus, mutta ne kaikki käyvät läpi ympyrän keskipisteen. Siten mikä tahansa viiva, joka sisältää ympyrän halkaisijan, on symmetrian akseli.

Joten, koska ympyrällä on ääretön määrä halkaisijoita, siinä on ääretön määrä symmetria-akseleita.

Muilla geometrisilla kuvioilla, kuten kolmio, nelikulmainen, viisikulmio, kuusikulmio tai mikä tahansa muu monikulmio, on rajallinen määrä symmetria-akseleita.

Syy, miksi ympyrällä on ääretön määrä symmetria-akseleita, on se, ettei sillä ole puolia.

viittaukset

1. Basto, J. R. (2014). Matematiikka 3: Analyyttinen geometria. Patrian toimittajaryhmä.
2. Billstein, R., Libeskind, S., & Lott, J. W. (2013). Matematiikka: perusopetuksen opettajien ongelmanratkaisu. López Mateos Editorit.
3. Bult, B., & Hobbs, D. (2001). Matematiikan sanakirja (kuvitettu ed.). (F. P. Cadena, Trad.) Julkaisut AKAL.
4. Callejo, I., Aguilera, M., Martinez, L., & Aldea, C. (1986). Math. Geometria. E.G.B: n ylemmän syklin uudistaminen. Opetusministeriö.
5. Schneider, W. & Sappert, D. (1990). Käytännön tekninen piirustusopas: johdanto teollisen teknisen piirustuksen perusteisiin. Reverte.
6. Thomas, G. B., ja Weir, M. D. (2006). Laskeminen: useita muuttujia. Pearson Education.