Kuinka monta reunaa on kuusikulmainen prisma?
Tiedä kuinka monta reunaa on kuusikulmainen prisma "reunan", "prisman" ja "kuusikulmaisen" merkityksen on oltava tiedossa. Kaksi ensimmäistä käsitettä ovat yleisiä määritelmiä, ja kolmas käsite liittyy geometrisen kuvion muotoon.
Kun puhutaan kuusikulmaisesta, mainitaan kuusikulma (monikulmio). Etuliite "hexa" osoittaa, että monikulmiossa on kuusi sivua.

Reuna on objektin reuna. Geometrisesti se on linja, joka yhdistää kaksi peräkkäistä geometrisen kuvan huippua.
Prisma on geometrinen kuva, joka on rajoitettu kahdella rinnakkaisella ja yhtäläisellä polygonilla olevalla pohjalla, ja niiden sivupinnat ovat rinnakkaismuotoisia.
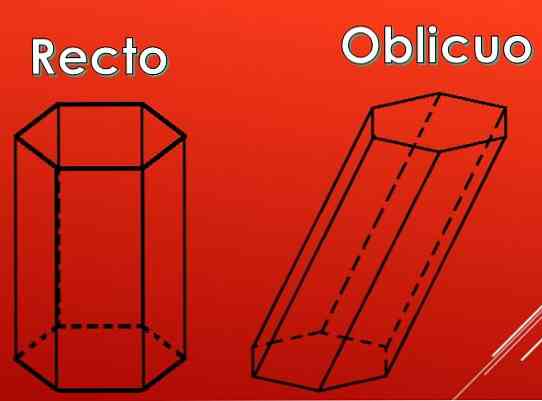
Seuraavassa kuvassa voidaan nähdä, että kuusikulmaisen prisman sivupinnat voivat olla suorakulmioita, mutta ne voivat olla myös rinnakkaismuotoja.
Rinnakkaismallien tyypin mukaan palkkiot voidaan luokitella kahteen tyyppiin: suora ja viisto.
Miten lasketaan kuusikulmaisen prisman reunat?
Kuusikulmaisen prisman reunojen määrä ei muutu, jos se on suora tai viisto prisma. Myös reunojen lukumäärä ei riipu sivujen pituudesta.
Kuusikulmaisen prisman reunojen laskeminen voidaan tehdä useilla tavoilla. Tässä on kaksi tapaa:
1- Hajota prisma
Yksi tapa laskea reunat on hajottaa kuusikulmainen prisma sen kahdessa pohjassa ja sen sivupinnoilla. Tällä tavalla saat kaksi kuusikulmioa ja rinnakkaismittarin, jossa on viisi sisäistä viivaa.
Kussakin kuusikulmiossa on kuusi reunaa, joten prismassa on yli 12 reunaa.
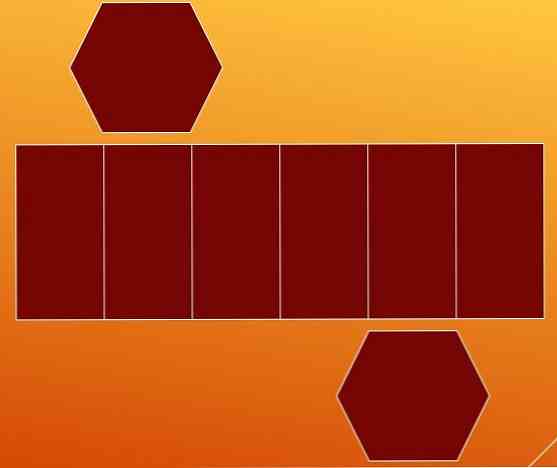
Ensi silmäyksellä ajatellaan, että rinnanogrammi sisältää yhdeksän reunaa (seitsemän pystysuoraa ja kaksi vaakasuoraa). Mutta on asianmukaista lopettaa analysoiminen tässä tapauksessa.
Kun rinnakkaiskaavio on taivutettu muodostamaan prisma, voidaan nähdä, että ensimmäinen rivi vasemmalla liittyy viimeiseen riviin oikealla, jolla molemmat linjat edustavat yhtä reunaa.
Mutta entä nämä kaksi vaakasuoraa viivaa?
Kun kaikki kappaleet kootaan uudelleen, vaakasuorat viivat liitetään kukin kuuden kuusikulmion kuusi reunaa vasten. Tästä syystä niiden laskeminen erikseen olisi virhe.
Niinpä rinnakkaiskaavio sisältää kuusi prismaa, jotka yhdessä alussa laskettujen 12 reunan kanssa antavat yhteensä 18 reunaa.
2.- Kunkin reunan heijastaminen
Toinen tapa, monta yksinkertaisempaa reunojen laskemiseen, on se, että kuusikulmaisten prismojen pohja on kuusikulmio, sitten jokaisella pohjalla on kuusi reunaa.
Toisaalta, kuusikulmion jokaisesta kärjestä, heijastetaan yksi reuna toisen kuusikulmion vastaavaan pisteeseen; toisin sanoen on olemassa kuusi reunaa, jotka yhdistävät yhden pohjan toiseen.
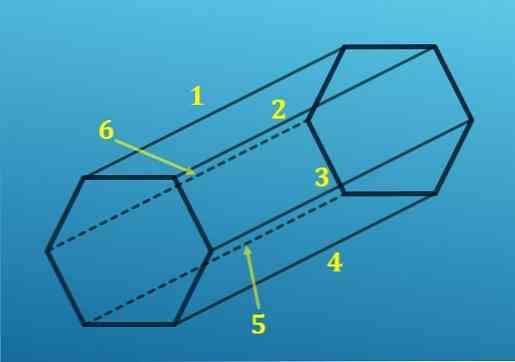
Lisäämällä kaikki reunat saat yhteensä 18 reunaa.
johtopäätös
Voidaan osoittaa, että prisman reunojen lukumäärä on kolminkertainen niiden reunojen lukumäärään, joita sen muodostamassa polygonissa on.
Siksi viisikulmaisessa prismassa on 3 * 5 = 15 reunaa, ja heptaalisessa prismassa on 3 * 7 = 21 reunaa ja siten sitä voidaan soveltaa mihin tahansa prismaan.
viittaukset
- Billstein, R., Libeskind, S., & Lott, J. W. (2013). Matematiikka: perusopetuksen opettajien ongelmanratkaisu. López Mateos Editorit.
- Fregoso, R. S., & Carrera, S. A. (2005). Matematiikka 3. Toimituksellinen Progreso.
- Gallardo, G., ja Pilar, P. M. (2005). Matematiikka 6. Toimituksellinen Progreso.
- Gutiérrez, C. T. ja Cisneros, M. P. (2005). 3. matematiikan kurssi. Toimituksellinen Progreso.
- Kinsey, L., & Moore, T. E. (2006). Symmetria, muoto ja tila: Johdatus matematiikkaan geometrian kautta (havainnollistettu, uusintapainos.). Springer Science & Business Media.
- Mitchell, C. (1999). Häikäisevät Math Line -mallit (Illustrated ed.). Scholastic Inc.
- R., M. P. (2005). Piirrän 6º. Toimituksellinen Progreso.


